Sejarah Geometri Euclid

GEOMETRI

Definisi Geometri

Salah satu cabang dari Matematika adalah Geometri. Geometri berasal dari bahasa Yunani yaitu geo yang artinya bumi dan metro yang artinya mengukur. Geometri adalah cabang Matematika yang pertama kali diperkenalkan oleh Thales (624-547 SM) yang berkenaan dengan relasi ruang. Dari pengalaman, atau intuisi, kita mencirikan ruang dengan kualitas fundamental tertentu, yang disebut aksioma dalam geometri. Aksioma demikian tidak berlaku terhadap pembuktian, tetapi dapat digunakan bersama dengan definisi matematika untuk titik, garis lurus, kurva, permukaan dan ruang untuk menggambarkan kesimpulan logis.

Menurut Novelisa Sondang  bahwa “Geometri menjadi salah satu ilmu Matematika yang diterapkan dalam dunia arsitektur; juga merupakan salah satu cabang ilmu yang berkaitan dengan bentuk, komposisi, dan proporsi.” Muhamad Fakhri Aulia menyebutkan bahwa  geometri dalam pengertian dasar adalah sebuah cabang ilmu yang mempelajari pengukuran bumi dan proyeksinya dalam sebuah bidang dua dimensi.

Alders (1961) menyatakan bahwa ”Geometri adalah salah satu cabang Matematika yang mempelajari tentang titik, garis, bidang dan benda-benda ruang beserta sifat-sifatnya, ukuran-ukurannya, dan hubungannya antara yang satu dengan yang lain.”

Dari beberapa definisi Geometri di atas dapat disimpulkan bahwa Geometri adalah salah satu cabang Matematika yang mempelajari tentang bentuk, ruang, komposisi beserta sifat-sifatnya, ukuran-ukurannya dan hubungan antara yang satu dengan yang lain.

Geometri Sulit?

Di bangku sekolah dasar maupun menengah seperti, SD/MI, SMP/MTs, SMA/MA atau SMK/MAK, materi geometri tidak diajarkan secara khusus, namun materi itu ada dalam satu kesatuan mata pelajaran matematika. dalam kurikulum matematika yang membahas mengenai geometri adalah pada bagian yang membahas mengenai bentuk, bangun ruang, sudut dan sebagainya sebagaimana yang sudah disampaikan di atas. Jika kita sedang mempelajari Dimensi 3, yang meliputi balok, kubus, volume dan sebagainya, berarti kita juga sedang mempelajarai geometri. Pada pokok bahasan inilah (Dimensi 3) seorang guru biasanya mengalami kesulitan untuk menjelaskannya kepada siswa. Mengapa? Kerena materi ini membutuhkan kemampuan visualisasi siswa yang relative tinggi. Sebagai contoh ketika siswa menjumpai soal dimensi 3 dimana siswa diminta untuk mencari panjang garis yang menghubungkan titik tengah  2 diagonal ruang suatu balok. Jika tidak ada alat peraga atau media pembelajaran, tentu tidak semua siswa mampu memvisualisasikannya. Nah, saat itulah para siswa dituntut untuk membayangkan sebuah bangun agar bisa memecahkan soal.  Tidak hanya masalah kemampuan memvisualisasikan, namun juga pemahaman siswa akan istilah rusuk dan rangka juga ternyata bermasalah. Ini dialami oleh para siswa di tingkat pendidikan dasar. Sebagaimana disampaikan oleh Wahyu Setiawan (1996 :4-5) bahwa daya serap siswa kelas IV Sekolah Dasar terhadap konsep-konsep volume rendah. Selain itu Soedjadi (1995) juga mengungkapkan bahwa masih banyak siswa yang mengalami miskonsepsi, misalnya ”siswa menyebut rusuk pada bangun ruang merupakan rangka yang menopang tubuh”.

Mahasiswa di jenjang pendidikan tinggi pun ternyata juga mengalami kesulitan dalam memahami materi. Ini diindikasikan dengan rendahnya prestasi belajar geometri mahasiswa. Seperti yang terjadi di prodi pendidikan matematika suatu universitas. Prosentasi kelulusan mahasiswa universitas tersebut dalam mengikuti perkuliahan geometri hanya mencapai ± 55 % – 65 %, dan sebagian besar yang lulus mendapat C. Prosentasi ini relatif rendah dibandingkan mata kuliah yang lain. Ini menjadi salah satu indikator bahwa materi Geometri memang relatif sulit untuk dipelajari.

Alternatif Solusi

Sebagai guru Matematika, tentu kita berusaha keras agar sesulit apapun materi matematika, siswa mampu memahaminya dengan mudah. Berbagai alat peraga atau media pembelajaran serta metode pun diterapkan di kelas agar kompetensi dasar dapat tercapai secara tuntas.

Dewasa ini kita mengenal adanya alat peraga tiga dimensi yang bisa memvisualisasikan secara gamblang bagaimana wujud tiga dimensi beserta sudut-sudut yang ada di dalamnya. Misal bangun kubus atau balok yang kita buat dari kertas karton. Namun kelemahan dari alat peraga ini, kita tidak akan mampu melihat titik sudut yang ada di dalam balok atau kubus tersebut. Dan ketika ada soal yang menghendaki besarnya sudut yang diapit oleh dua garis diagonal ruang, maka tidak banyak siswa yang mampu memvisualisasikannya jika menggunakan alat peraga ini. Kecuali jika kubus atau balok itu dalam keadaan terbuka.

Di samping alat peraga yang terbuat dari kertas, ada juga alat peraga bangun ruang yang terbuat dari kaca, atau bahan seperti mika. Tentu ini akan sangat membantu siswa untuk bisa memvisualisasikan besarnya sudut yang diapit oleh dua diagonal ruang.

Selain kedua alat peraga di atas, kita bisa juga menggunakan alat peraga berbasis IT. Ada beberapa alat peraga yang biasa kita kenal yaitu Microsoft Power Point dan Macromedia Flash. Selain kedua alat peraga itu, ada alat peraga yag sangat memudahkan kita dalam menggambarkan bangun tiga dimensi yang ukurannya bisa sesuai dengan keinginan kita. Keakuratan ukurannya sangat tinggi. Tinggal meng ‘klik’ tombol tertentu, kita akan mendapatkan gambar bangun tiga dimensi sesuai dengan yang kita inginkan.Warna gambar juga tentu bisa kita atur. Alat peraga ini berupa software yang yang dinamai Cabri 3d. Kita mungkin akan banyak menjumpai software Macromedia Flash, tapi tidak bagi software Cabri 3d. Software ini tidak beredar luas.

GEOMETRI EUCLID

Euclid

Tidak banyak orang yang beruntung memperoleh kemasyhuran yang abadi seperti Euclid, ahli ilmu ukur Yunani yang besar. Meskipun semasa hidupnya tokoh-tokoh seperti Napoleon, Martin Luther, Alexander yang Agung, jauh lebih terkenal ketimbang Euclid tetapi dalam jangka panjang ketenarannya mungkin mengungguli semua mereka yang disebut itu.

Selain kemasyhurannya, hampir tak ada keterangan terperinci mengenai kehidupan Euclid yang bisa diketahui. Misalnya, kita tahu dia pernah aktif sebagai guru di Iskandariah, Mesir, di sekitar tahun 300 SM, tetapi kapan dia lahir dan kapan dia wafat betul-betul gelap. Bahkan, kita tidak tahu di benua apa dan dikota apa dia dilahirkan. Meski dia menulis beberapa buku dan diantaranya masih ada yang tertinggal, kedudukannya dalam sejarah terutama terletak pada bukunya yang hebat mengenai ilmu ukur yang bernama The Elements.

Arti penting buku The Elements tidaklah terletak pada pernyataan rumus-rumus pribadi yang dilontarkannya. Hampir semua teori yang terdapat dalam buku itu sudah pernah ditulis orang sebelumnya, dan juga sudah dapat dibuktikan kebenarannya. Sumbangan Euclid terletak pada cara pengaturan dari bahan-bahan dan permasalahan serta formulasinya secara menyeluruh dalam perencanaan penyusunan buku. Di sini tersangkut, yang paling utama, pemilihan dalil-dalil serta perhitungan-perhitungannya, misalnya tentang kemungkinan menarik garis lurus diantara dua titik. Sesudah itu dengan cermat dan hati-hati dia mengatur dalil sehingga mudah difahami oleh orang-orang sesudahnya. Bilamana perlu, dia menyediakan petunjuk cara pemecahan hal-hal yang belum terpecahkan dan mengembangkan percobaan-percobaan terhadap permasalahan yang terlewatkan. Perlu dicatat bahwa buku The Elements selain terutama merupakan pengembangan dari bidang geometri yang ketat, juga di samping itu mengandung bagian-bagian soal aljabar yang luas berikut teori penjumlahan.

Buku The Elements sudah merupakan buku pegangan baku lebih dari 2000 tahun dan tak syak lagi merupakan buku yang paling sukses yang pernah disusun manusia. Begitu hebatnya Euclid menyusun bukunya sehingga dari bentuknya saja sudah mampu menyisihkan semua buku yang pernah dibuat orang sebelumnya dan yang tak pernah digubris lagi. Aslinya ditulis dalam bahasa Yunani, kemudian buku The Elements itu diterjemahkan ke dalam berbagai bahasa. Terbitan pertama muncul tahun 1482, sekitar 30 tahun sebelum penemuan mesin cetak oleh Gutenberg. Sejak penemuan mesin itu dicetak dan diterbitkanlah dalam beribu-ribu edisi yang beragam corak.

Sebagai alat pelatih logika pikiran manusia, buku The Elements jauh lebih berpengaruh ketimbang semua risalah Aristoteles tentang logika. Buku itu merupakan contoh yang komplit sekitar struktur deduktif dan sekaligus merupakan buah pikir yang menakjubkan dari semua hasil kreasi otak manusia.

Adalah adil jika kita mengatakan bahwa buku Euclid merupakan faktor penting bagi pertumbuhan ilmu pengetahuan modern. Ilmu pengetahuan bukanlah sekedar kumpulan dari pengamatan-pengamatan yang cermat dan bukan pula sekedar generalisasi yang tajam serta bijak. Hasil besar yang direnggut ilmu pengetahuan modern berasal dari kombinasi antara kerja penyelidikan empiris dan percobaan-percobaan di satu pihak, dengan analisa hati-hati dan kesimpulan yang punya dasar kuat di lain pihak.

Kita masih bertanya-tanya apa sebab ilmu pengetahuan muncul di Eropa dan bukan di Cina, tetapi rasanya aman jika kita menganggap bahwa hal itu bukanlah semata-mata lantaran soal kebetulan. Memanglah, peranan yang digerakkan oleh orang-orang brilian seperti Newton, Galileo dan Copernicus mempunyai makna yang teramat penting. Tetapi, tentu ada sebab-musababnya mengapa orang-orang ini muncul di Eropa. Mungkin sekali faktor historis yang paling menonjol apa sebab mempengaruhi Eropa dalam segi ilmu pengetahuan adalah rasionalisme Yunani, bersamaan dengan pengetahuan matematika yang diwariskan oleh Yunani kepada Eropa. Patut kiranya dicatat bahwa Cina --meskipun berabad-abad lamanya teknologinya jauh lebih maju ketimbang Eropa-- tak pernah memiliki struktur matematika teoritis seperti halnya yang dipunyai Eropa. Tak ada seorang matematikus Cina pun yang punya hubungan dengan Euclid. Orang-orang Cina menguasai pengetahuan yang bagus tentang ilmu geometri praktis, tetapi pengetahuan geometri mereka tak pernah dirumuskan dalam suatu skema yang mengandung kesimpulan.

Bagi orang-orang Eropa, anggapan bahwa ada beberapa dasar prinsip-prinsip fisika yang dari padanya semuanya berasal, tampaknya hal yang wajar karena mereka punya contoh Euclid yang berada di belakang mereka. Pada umumnya orang Eropa tidak beranggapan geometrinya Euclid hanyalah sebuah sistem abstrak, melainkan mereka yakin benar bahwa gagasan Euclid --dan dengan sendirinya teori euclid-- memang benar-benar merupakan kenyataan yang sesungguhnya.

Pengaruh Euclid terhadap Sir Isaac Newton sangat kentara sekali, sejak Newton menulis buku tersohornya The Principia dalam bentuk kegeometrian, mirip dengan The Elements. Berbagai ilmuwan mencoba menyamakan diri dengan Euclid dengan jalan memperlihatkan bagaimana semua kesimpulan mereka secara logis berasal mula dari asumsi asli. Tak kecuali apa yang diperbuat oleh ahli matematika seperti Russel, Whitehead dan filosof Spinoza.

Kini, para ahli matematika sudah memaklumi bahwa geometri Euclid . bukan satu-satunya sistem geometri yang memang jadi pegangan pokok dan teguh serta yang dapat direncanakan pula, mereka pun maklum bahwa selama 150 tahun terakhir banyak orang yang merumuskan geometri bukan a la Euclid. Sebenarnya, sejak teori relativitas Einstein diterima orang, para ilmuwan menyadari bahwa geometri Euclid tidaklah selamanya benar dalam penerapan masalah cakrawala yang sesungguhnya. Pada kedekatan sekitar "Lubang hitam" dan bintang neutron --misalnya-- dimana gayaberat berada dalam derajat tinggi, geometri Euclid tidak memberi gambaran yang teliti tentang dunia, ataupun tidak menunjukkan penjabaran yang tepat mengenai ruang angkasa secara keseluruhan. Tetapi, contoh-contoh ini langka, karena dalam banyak hal pekerjaan Euclid menyediakan kemungkinan perkiraan yang mendekati kenyataan. Kemajuan ilmu pengetahuan manusia belakangan ini tidak mengurangi baik hasil upaya intelektual Euclid maupun dari arti penting kedudukannya dalam sejarah.

Sejarah Geometri Euclid

Geometri Euclidean adalah sistem matematika yang dikaitkan dengan Alexandria matematikawan Yunani Euclid , yang dijelaskan dalam buku teks tentang geometri yaitu Elements . Metode Euclid terdiri dalam asumsi satu set kecil intuitif menarik aksioma , dan menyimpulkan lainnya proposisi ( dalil ) dari ini. Meskipun banyak dari hasil Euclid telah dinyatakan oleh matematikawan sebelumnya, Euclid adalah yang pertama untuk menunjukkan bagaimana proposisi-proposisi bisa masuk ke dalam deduktif dan komprehensif sistem logis . Unsur dimulai dengan pesawat geometri, masih diajarkan di sekolah menengah sebagai yang pertama sistem aksiomatik dan contoh pertama dari bukti formal . Berpindah ke geometri solid dari tiga dimensi . Banyak dari Elemen menyatakan hasil dari apa yang sekarang disebut aljabar dan nomor teori , ditulis dalam bahasa geometris.

Selama lebih dari dua ribu tahun, kata sifat "Euclid" tidak diperlukan karena tidak ada geometri lain yang disusun. Aksioma Euclid nampak seperti sangat jelas bahwa pembuktian teorema lainnya dianggap benar dalam arti, mutlak sering metafisik,. Namun, sekarang banyak lainnya konsisten diri non-Euclidean geometri diketahui, yang pertama yang telah ditemukan pada awal abad 19. Implikasi dari Einstein teori relativitas umum adalah bahwa ruang Euclidean adalah pendekatan yang baik terhadap sifat ruang fisik hanya di mana medan gravitasi tidak terlalu kuat. 

Unsur

Unsur terutama sebuah sistematisasi pengetahuan awal geometri. Keunggulannya di atas perawatan sebelumnya dengan cepat diakui, dengan hasil bahwa ada sedikit minat dalam melestarikan yang sebelumnya, dan mereka sekarang hampir semua hilang.

Buku I-IV dan VI membahas geometri bidang datar. Banyak hasil tentang tokoh-tokoh pesawat terbukti, misalnya, Jika segitiga memiliki dua sudut yang sama, maka sisi  yang bersesuaian dengan sudut tersebut adalah sama . Teorema Pythagoras terbukti.

Buku V dan VII-X berurusan dengan nomor teori, dengan nomor diperlakukan secara geometris melalui representasi mereka sebagai segmen garis dengan berbagai panjang. Pengertian seperti bilangan prima dan rasional dan bilangan irasional diperkenalkan. Yang tak terbatas bilangan prima terbukti.

Buku XI-XIII geometri perhatian padat. Hasil khas adalah rasio 01:03 antara volume kerucut dan silinder dengan ketinggian yang sama dan basis.

Persamaan postulat: Jika dua garis berpotongan sepertiga sedemikian rupa sehingga jumlah dari sudut-sudut bagian dalam di satu sisi kurang dari dua sudut yang tepat, maka mau tidak mau harus dua baris saling berpotongan pada sisi jika diperpanjang cukup jauh.

Aksioma

Geometri Euclidean adalah sistem aksiomatik , di mana semua teorema ("pernyataan benar") berasal dari sejumlah kecil aksioma. Menjelang awal buku pertama dari Elemen, Euclid memberikan lima postulat (aksioma) untuk pesawat geometri , menyatakan dalam hal konstruksi (sebagaimana diterjemahkan oleh Thomas Heath):

"Mari berikut akan mendalilkan":

1.     "Untuk menggambar garis lurus dari setiap titik ke titik apapun. "

2. "Untuk menghasilkan [memperluas] sebuah garis lurus yang terbatas terus menerus dalam garis lurus. "

3.     "Untuk menggambarkan lingkaran dengan pusat dan jarak [radius]. "

4.     "Itu semua sudut yang tepat sama dengan satu sama lain."

5.     Para paralel dalil : "Itu, jika garis lurus jatuh di dua jalur lurus membuat sudut interior pada sisi yang sama kurang dari dua sudut yang tepat, dua garis lurus, jika diproduksi tanpa batas waktu, bertemu di sisi itu yang adalah sudut kurang dari dua sudut yang tepat. "

Meskipun pernyataan Euclid dari postulat hanya secara eksplisit menegaskan keberadaan konstruksi, mereka juga diambil untuk menjadi unik.

Elements juga memasukkan lima "notasi biasa":

1.     Hal-hal yang sama dengan hal yang sama juga sama satu dengan lainnya.

2.     Jika sesuatu yang sama ditambahkan ke sama, maka keutuhan adalah sama.

3.     Jika sesuatu yang sama dikurangkan dari sama, maka sisanya adalah sama.

4.     Hal-hal yang bertepatan dengan satu sama lain sama satu sama lain.

5.     Keseluruhan lebih besar daripada bagian.

Paralel postulat

Untuk nenek moyang, paralel  tampak kurang jelas mendalilkan dari yang lain. Euclid sendiri tampaknya telah dianggap sebagai yang secara kualitatif berbeda dari yang lain, sebagaimana dibuktikan oleh organisasi dari Elemen: 28 yang pertama ia menyajikan proposisi adalah mereka yang dapat dibuktikan tanpa itu.

Aksioma banyak alternatif dapat dirumuskan yang sama konsekuensi logis sebagai paralel dalil. Misalnya aksioma Playfair 's menyatakan:

Dalam pesawat, melalui titik tidak pada garis lurus yang diberikan, paling banyak satu baris dapat ditarik bahwa tidak pernah memenuhi garis yang diberikan.

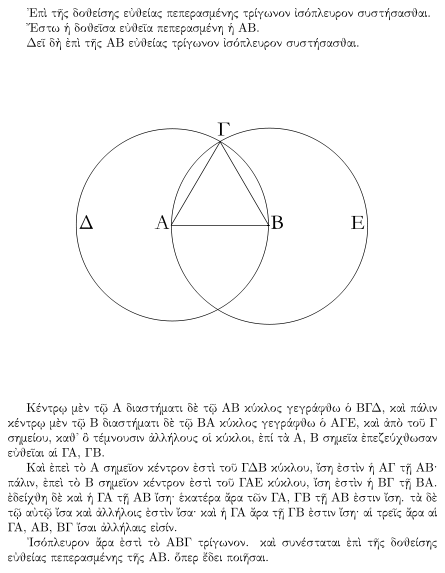
Sebuah bukti dari elemen Euclid bahwa, mengingat segmen garis, segitiga sama sisi ada yang mencakup segmen sebagai salah satu sisinya. Buktinya adalah dengan mengkonstruksi sebuah segitiga sama sisi ΑΒΓ dibuat dengan menggambar lingkaran dan Δ Ε berpusat pada poin Α dan Β, dan mengambil satu persimpangan lingkaran sebagai titik ketiga dari segitiga.

Metode pembuktian

Geometri Euclid adalah konstruktif . Postulat 1, 2, 3, dan 5 menegaskan bahwa keberadaan dan keunikan dari bidang geometri tertentu, dan penegasan ini adalah konstruksi alam: yaitu, kita tidak diberitahu bahwa sesuatu itu ada, tetapi juga kita diberikan metode untuk membuatnya dengan lebih dari satu tidak ada kompas dan lurus yang tidak bertanda . Dalam hal ini, geometri Euclid adalah lebih konkrit daripada kebanyakan sistem aksiomatik modern seperti teori set , dimana sering menegaskan keberadaan objek tanpa memberitahukan bagaimana mengkonstruksi mereka, atau menegaskan keberadaan objek yang tidak dapat dibangun dalam teori. Tepatnya, garis-garis pada kertas model dari objek didefinisikan dalam sistem formal, bukan contoh objek tersebut. Misalnya garis lurus Euclidean memiliki lebar  atau tidak, tetapi setiap garis yang ditarik akan nyata . Meskipun hampir semua matematikawan modern yang mempertimbangkan metode nonconstructive hanya sebagai suara yang konstruktif, bukti konstruktif Euclid sering diartikan keliru sebagai metode nonconstructive misalnya, beberapa bukti Pythagorean   nomor  irasional yang terlibat, yang biasanya diperlukan pernyataan seperti "Cari ukuran umum terbesar dari ... "

Euclid sering digunakan bukti oleh kontradiksi . Geometri Euclidean juga memungkinkan metode superposisi, di mana angka ditransfer ke titik lain di ruang angkasa. Misalnya, proposisi I.4, pada kongruensi segitiga dengan aksioma sisi-sudut-sisi, terbukti dengan memindahkan salah satu dari dua segitiga sehingga salah satu sisinya bertepatan dengan sisi segitiga sama lain, dan kemudian membuktikan bahwa sisi lain bertepatan juga . Beberapa perawatan modern menambahkan seperenam postulat, kekakuan segitiga, yang dapat digunakan sebagai alternatif untuk superposisi.

Sistem pengukuran dan aritmatika

Geometri Euclidean memiliki dua tipe dasar pengukuran: sudut dan jarak. Skala sudut adalah mutlak, dan Euclid menggunakan sudut yang tepat sebagai unit dasarnya, sehingga, misalnya, sebuah sudut 45 derajat akan disebut sebagai setengah dari sudut kanan. Skala jarak relatif, satu sewenang-wenang mengambil segmen garis dengan panjang tertentu sebagai unit, dan jarak lainnya disajikan dalam kaitannya dengan hal itu.

Sebuah garis dalam geometri Euclidean adalah model garis bilangan real . Sebuah segmen garis adalah bagian dari garis yang dibatasi oleh dua titik akhir, dan berisi setiap titik pada garis antara titik akhir. Penambahan diwakili oleh konstruksi di mana satu segmen garis akan disalin ke akhir dari suatu segmen garis untuk memperpanjang panjangnya, dan juga untuk pengurangan.

Pengukuran luas dan volume berasal dari jarak. Sebagai contoh, sebuah persegi panjang dengan lebar 3 dan panjang 4 memiliki luas yang mewakili produk, 12. Karena interpretasi geometris dari perkalian terbatas pada tiga dimensi, tidak ada cara langsung menafsirkan produk dari empat atau lebih angka, dan Euclid dihindari produk tersebut, meskipun mereka tersirat, misalnya, dalam bukti buku IX, proposisi 20.

Contoh kongruensi. Dua angka di sebelah kiri adalah kongruen, sementara yang ketiga adalah serupa kepada mereka. Angka terakhir adalah tidak. Perhatikan bahwa  kongruensi mengubah beberapa sifat, seperti lokasi dan orientasi, tetapi membiarkan yang lain tidak berubah, seperti jarak dan sudut . Jenis kedua sifat ini disebut invariants dan pelajaran itu adalah inti dari geometri.

Euclid mengacu pada sepasang garis, atau sepasang bangun planar atau padat, sebagai "sama" (ἴσος) jika panjang mereka, daerah, atau volume adalah sama, dan juga untuk sudut. Istilah lebih kuat " kongruen "mengacu pada ide bahwa  bangun dengan seluruh ukuran yang sama dan bentuk sebagai bentuk lain. Atau, dua bangun yang kongruen jika bangun tersebut dapat dipindahkan di atas yang lain sehingga cocok dengan persis. (Flipping di atas diperbolehkan.) Jadi, misalnya, persegi panjang 2x6 dan 3x4 persegi panjang adalah sama tetapi tidak kongruen, dan huruf R adalah kongruen dengan bayangannya. Angka yang akan kongruen kecuali untuk ukuran mereka yang berbeda disebut sebagai serupa.

Notasi dan terminologi

Penamaan poin dan angka

Poin lazim diberi nama menggunakan huruf alfabet. Objek lainnya, seperti garis, segitiga, atau lingkaran, diberi nama dengan daftar cukup banyak poin untuk menjemput mereka keluar jelas dari angka yang relevan, misalnya, segitiga ABC biasanya akan menjadi segitiga dengan simpul pada titik-titik A, B, dan C .

sudut pelengkap dan penunjang

Sudut yang jumlahnya 90 derajat adalah sudut siku-siku disebut komplementer , sedangkan sudut yang jumlahnya 180 derajat adalah sudut lurus adalah tambahan (suplementer).

Versi Modern notasi Euclid

Dalam terminologi modern, sudut biasanya akan diukur dalam derajat atau radian .

Buku pelajaran sekolah modern sering mendefinisikan bangun terpisah yang disebut baris (tak terbatas), sinar (semi-infinite), dan segmen garis (panjang terbatas). Euclid, daripada membahas sebuah sinar sebagai objek yang meluas hingga tak terbatas dalam satu arah, biasanya akan menggunakan lokusi seperti "jika baris ini diperpanjang dengan panjang yang cukup," meskipun ia kadang-kadang disebut "garis yang tak terbatas." Sebuah "garis" dalam Euclid dapat berupa lurus atau melengkung, dan ia menggunakan istilah yang lebih spesifik "garis lurus" bila diperlukan.

Beberapa hasil penting atau terkenal

• Teorema Jembatan keledai  menyatakan bahwa A = B dan C = D.

• Jumlah dari sudut A, B, dan C adalah sama dengan 180 derajat. 

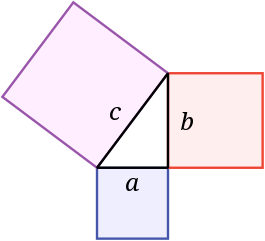
• Teorema Pythagoras: Jumlah dari bidang dua kotak pada kaki (a dan b) dari sebuah segitiga siku-siku sama dengan luas persegi pada sisi miring (c).

 

• Teorema Thales: jika AC adalah diameter, maka sudut di B adalah sudut kanan.

Jembatan Menilai

Jembatan menilai (Pons Asinorum) menyatakan bahwa dalam segitiga sama kaki sudut di dasar sama satu sama lain, dan, jika garis-garis lurus yang sama yang diproduksi lebih lanjut, maka sudut bawah dasar sama satu sama lain. Namanya mungkin dikaitkan dengan peran sering sebagai tes nyata pertama dalam Unsur-unsur kecerdasan pembaca dan sebagai jembatan untuk proposisi keras yang diikuti. Hal ini juga mungkin dinamakan demikian karena kemiripannya sosok geometris untuk jembatan yang curam yang hanya seekor keledai yang dapat menyeberang.

Kongruensi segitiga

Kongruensi segitiga ditentukan dengan menentukan dua sisi dan sudut antara mereka (SAS), dua sudut dan sisi antara mereka (ASA) atau dua sudut dan sisi yang berdekatan sesuai (SSA). Menentukan dua sisi dan sudut yang berdekatan (SSA), bagaimanapun, dapat menghasilkan dua segitiga yang mungkin berbeda.

Segitiga dikatakan kongruen jika mereka memiliki ketiga sisi yang sama (SSS), dua sisi dan sudut antara mereka sama (SAS), atau dua sudut dan sisi yang sama (ASA) (Buku I, proposisi 4, 8, dan 26). (Segitiga dengan tiga sudut yang sama umumnya serupa, tetapi belum tentu kongruen Juga, segitiga dengan dua sisi yang sama dan sudut yang berdekatan tidak selalu sama..)

Jumlah sudut sebuah segitiga

Jumlah sudut sebuah segitiga sama dengan sudut lurus (180 derajat).

Teorema Pythagoras

Para terkenal Teorema Pythagoras  (buku I, proposisi 47) menyatakan bahwa dalam setiap segitiga siku-siku, luas persegi yang sisinya adalah sisi miring (sisi berlawanan sudut yang tepat) sama dengan jumlah dari bidang kotak yang sisi-sisinya  bertemu di sudut 90 derajat (kedua belah pihak yang bertemu di sudut kanan).

Thales 'Teorema

Thales 'Teorema , yaitu setelah Thales dari Miletus menyatakan bahwa jika A, B, dan C adalah titik pada lingkaran di mana garis AC adalah diameter lingkaran, maka sudut ABC adalah sudut kanan. Penyanyi menyangka bahwa Thales membuktikan Teorema melalui Euclid buku saya, prop 32 menurut cara Euclid buku III, prop 31. Tradisi mengatakan bahwa Thales mengorbankan lembu untuk merayakan teorema ini.

Scaling daerah dan volume

Dalam terminologi modern, area objek pesawat sebanding dengan kuadrat dari setiap dimensi linier. Dan volume yang solid untuk kubus. Euclid membuktikan hasil ini dalam berbagai kasus khusus seperti luas lingkaran  dan volume yang solid parallelepipedal. Euclid ditentukan, tapi tidak semua, dari konstanta proporsionalitas yang relevan. Misalnya, itu penggantinya Archimedes yang membuktikan bahwa bola memiliki 2/3 volume silinder circumscribing.

Aplikasi

Karena status dasar geometri Euclidean dalam matematika, tidak mungkin untuk memberikan lebih dari sampling wakil dari aplikasi di sini. 

Sebuah surveyor menggunakan Tingkat

 

Kemasan Sphere berlaku untuk tumpukan jeruk . 

Sebuah cermin parabola membawa sinar paralel dari cahaya untuk fokus. 

Seperti yang disarankan oleh etimologi kata, salah satu alasan paling awal untuk kepentingan dalam geometri itu survei , dan hasil praktis tertentu dari geometri Euclidean, seperti properti yang tepat-sudut segitiga 3-4-5, digunakan jauh sebelum mereka terbukti secara formal. Jenis-jenis dasar pengukuran dalam geometri Euclidean adalah jarak dan sudut, dan kedua kuantitas dapat diukur langsung oleh surveyor. Secara historis, jarak sering diukur dengan rantai seperti rantai Gunter itu , dan sudut menggunakan lingkaran lulus dan, kemudian, teodolit . 

Sebuah aplikasi dari geometri Euclidean yang solid adalah penentuan pengaturan kemasan , seperti masalah untuk menemukan yang paling efisien kemasan bola dalam dimensi n. Masalah ini memiliki aplikasi dalam deteksi dan koreksi kesalahan .

Optik geometris menggunakan geometri Euclidean untuk menganalisis fokus cahaya oleh lensa dan cermin. 

• Geometri digunakan dalam seni dan arsitektur.

• Menara air terdiri dari kerucut, silinder, dan  setengah bola. Volumenya dapat dihitung dengan menggunakan geometri padat.

• Geometri dapat digunakan untuk merancang origami.

Geometri digunakan secara luas dalam arsitektur .

Geometri dapat digunakan untuk merancang origami . Beberapa masalah konstruksi klasik geometri tidak mungkin menggunakan kompas dan penggaris-sejajar , tetapi dapat diselesaikan dengan menggunakan origami . 

LATIHAN SOAL !

1. Jelaskan definisi geometri !
2. Jelaskan pengertian sejarah geometri euclid !
3. Sebutkan dan jelaskan tipe-tipe dasar pengukuran dalam geometri euclid !
4. Sebutkan dan jelaskan notasi terminologi dalam geometri euclid !
5. Jelaskan tentang theorema pythagoras dan teorema Thales !
6. Jelaskan aplikasi dari geometri euclid dan berikan contoh !
7. Untuk menggambarkan pemecahan masalah secara memadai/membutuhkan sistem yang lebih kaya dan konsep logis kontras dalam pendekatan.Jelaskan !